[Paper Review] GaussCraft: Precision Editing and Reconstruction with 2D Gaussian Splatting
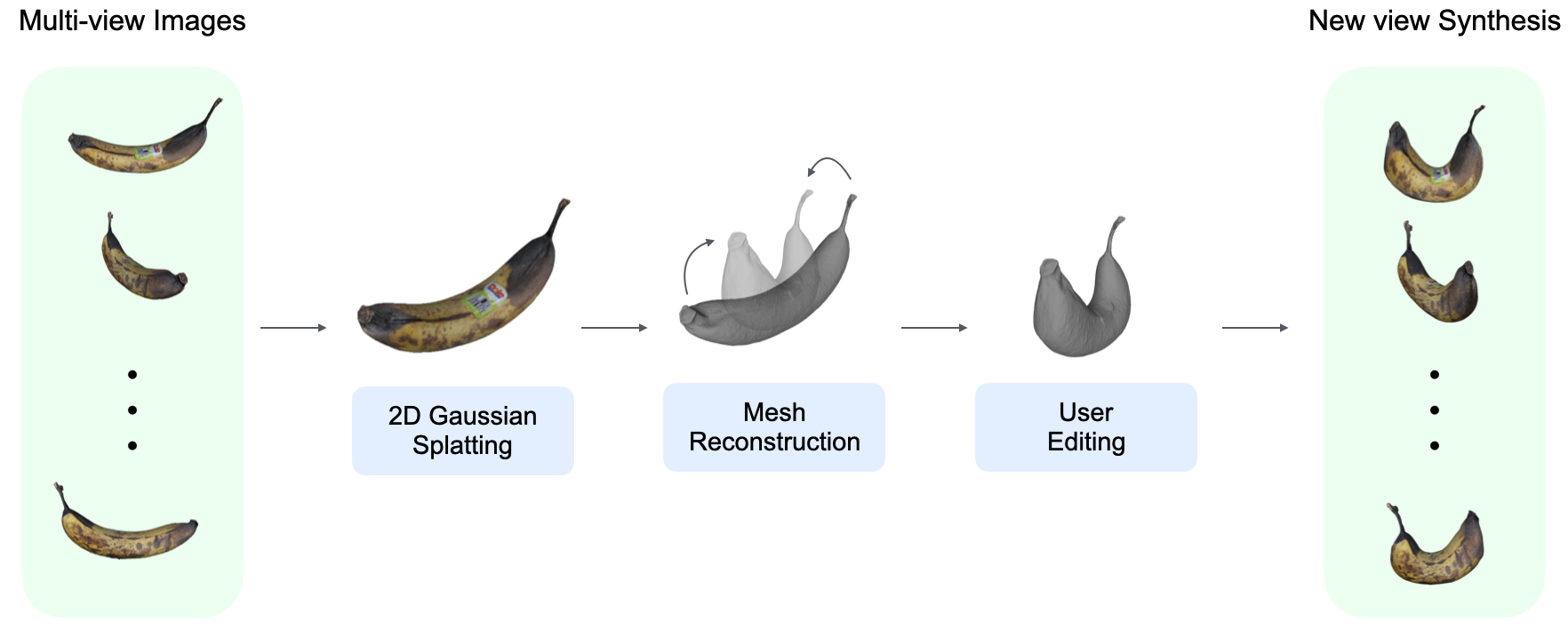
Introduction
In this post, I review GaussCraft: Precision Editing and Reconstruction with 2D Gaussian Splatting, my Master’s thesis conducted at University College London (UCL). This work introduces a real-time scene editing framework that leverages the geometric accuracy of 2D Gaussian Splatting for high-quality mesh reconstruction and deformation. Unlike previous implicit methods (NeRF) or avatar-specific Gaussian models, GaussCraft enables user-directed editing for general scenes without the need for retraining for each edited result.
Paper Info
- Title: GaussCraft: Precision Editing and Reconstruction with 2D Gaussian Splatting
- Author: Jiwon Park
- Supervisor: Prof. Lourdes Agapito
- Institution: University College London (UCL)
- Project page: GaussCraft
Motivation
Existing 2D or 3D Gaussian Splatting methods provide impressive reconstruction but lack the capacity for direct scene editing. Previous work has faced several hurdles:
- Implicit Editing Complexity: NeRF-based editing requires heavy computation and long training times.
- Avatar Limitations: Current Gaussian editing (like GaussianAvatars) is restricted to specific templates like FLAME and does not work for general scenes.
- Surface Inaccuracy: 3DGS often results in “cloud-like” artifacts that do not align well with physical surfaces during deformation.
GaussCraft addresses these by introducing a 2D Gaussian-to-mesh rigging framework for general, real-time deformation.
Method Overview
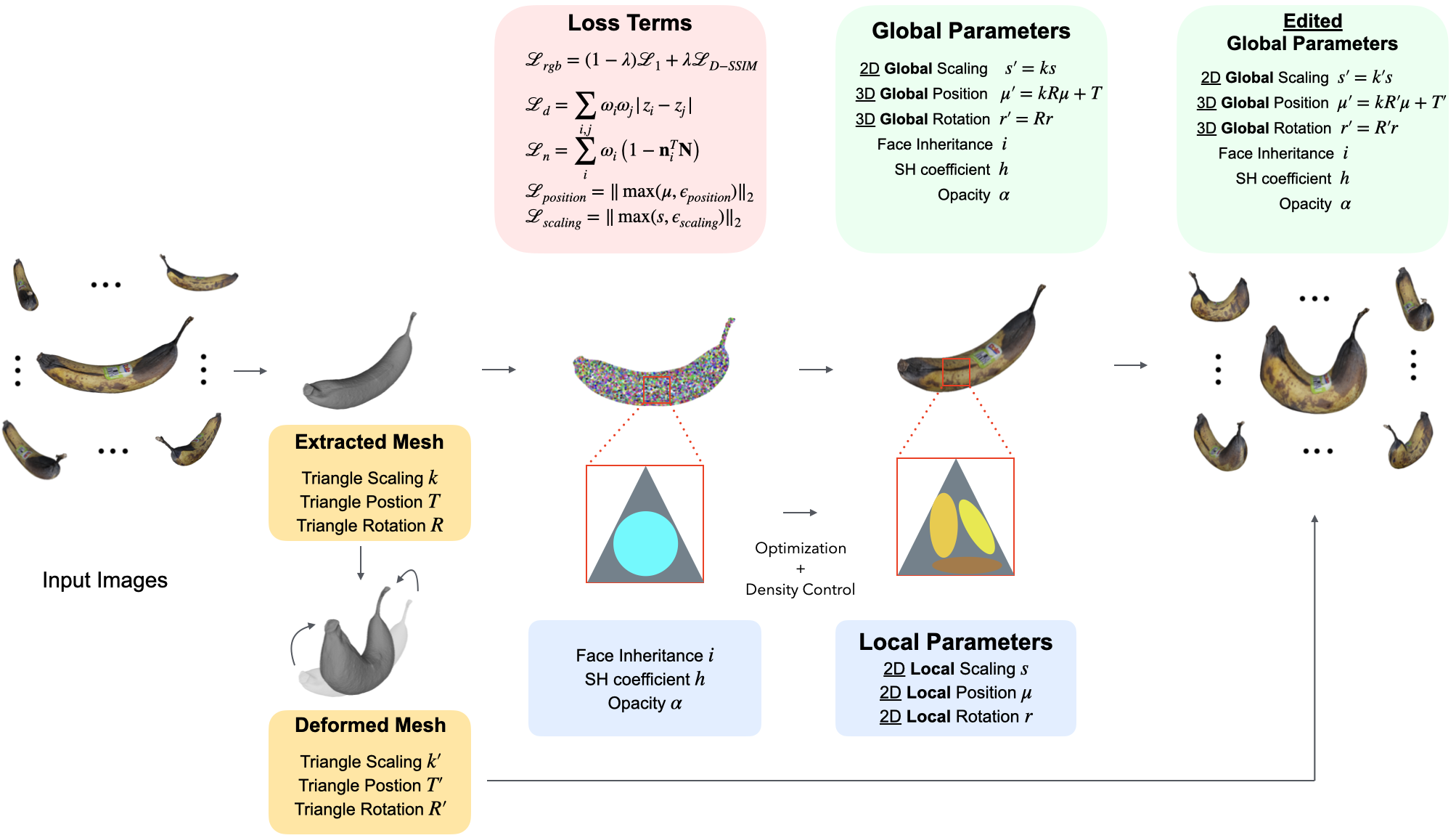
1. 2D Gaussian Rigging
GaussCraft bridges the gap between a reconstructed triangular mesh and 2D Gaussian splats. By treating each Gaussian as if it lives on the tangent plane of a specific mesh face, the framework effectively synthesizes the core concepts of Gaussian Avatar and 2D Gaussian Splatting. This design choice addresses a key limitation of 3DGS: while volumetric 3D Gaussians struggle to articulate cleanly along mesh surfaces, 2D Gaussians are inherently suited for surface-driven movement, ensuring structural coherence during editing.
🧱 Local Frame Construction
For each triangular face with vertices \(\{v_1, v_2, v_3\}\):
- The local origin T is the mean of the vertices.
- A rotation matrix \(R \in \mathbb{R}^{3 \times 3}\) is constructed using the edge direction, the face normal, and their cross product.
- The scale factor k is derived from the mean edge length and its perpendicular, ensuring the Gaussian remains relative to the triangle’s physical size.
🧩 Gaussian Parameters in Local Space
GaussCraft simplifies the transformation by removing the z-axis from local space. Each Gaussian is defined by:
- Local 2D position \(\mu\)
- Local 2D rotation \(r\)
- Local anisotropic scale \(s\)
At render time, these are projected into global space using the mesh’s current state:
\[r' = R \cdot r \\ \mu' = k \cdot R \cdot \mu + T \\ s' = k \cdot s\]By restricting the rotation and position to the local tangent plane, we significantly reduce artifacts and ensure the Gaussians follow the mesh deformation naturally.
2. Training Pipeline
Optimization involves balancing photometric accuracy with geometric constraints to ensure Gaussians do not drift away from the mesh during user editing.
📦 Overall Loss Function
The full optimization loss is:
\[\mathcal{L} = \mathcal{L}_{\text{rgb}} + \alpha \mathcal{L}_{\text{d}} + \beta \mathcal{L}_{\text{n}} + \gamma \mathcal{L}_{\text{p}} + \delta \mathcal{L}_{\text{s}}\]Where:
- \(\mathcal{L}_{\text{rgb}}\): Standard L1 + D-SSIM loss.
- \(\mathcal{L}_{\text{d}}\): Depth Distortion Loss to concentrate weight along rays.
- \(\mathcal{L}_{\text{n}}\): Normal Consistency Loss to align splat normals with surface geometry.
- \(\mathcal{L}_{\text{p}}\): Position Loss to prevent Gaussians from drifting off their parent triangle.
- \(\mathcal{L}_{\text{s}}\): Scale Loss to prevent jittering caused by oversized Gaussians.
🧬 Binding Inheritance (Adaptive Density Control)
To represent fine details like hair or textures, we use adaptive density control with a custom strategy:
- Densification: When a Gaussian is split or cloned, the new primitives inherit the index of the parent triangle.
- Pruning: Low-opacity Gaussians are removed, but a constraint ensures each triangle always maintains at least one Gaussian to prevent holes in the scene during editing.
- Outlier Removal: Any Gaussian that moves beyond a specific distance threshold from the mesh center is pruned to ensure stability.
3. User Editing via ARAP
Once the Gaussians are rigged, users can manipulate the mesh using As-Rigid-As-Possible (ARAP) deformation. Because the Gaussians are bound to the local space of the triangles, the global rendering updates in real-time as the vertices move, without requiring any further optimization.
Key Contributions
- Flexible Real-Time Editing: The first framework to enable general scene editing using 2D Gaussian Splatting and mesh deformation.
- 2D Dimensionality Simplification: Enhances consistency and reduces computational overhead by treating mesh faces as tangent planes.
- Binding Inheritance: A robust strategy to maintain geometric coherence during adaptive densification.
Results

- Performance: Achieves high-quality synthesis at ~15 FPS on a single RTX 3090 TI.
- Comparison: Outperforms NeRF-Editing in both speed (10 mins vs 16 hours training) and visual metrics (SSIM 0.96 vs 0.94).
- Versatility: Successfully tested on NeRF Synthetic, DTU, and Mixamo datasets, demonstrating stability in both synthetic and real-world captures.
Limitations and Future Work
- Static Lighting: Shadows and specularities remain baked into the Gaussians, which can look inconsistent after large deformations.
- Mesh Dependency: The quality is tied to the initial reconstructed mesh resolution.
Future work involves integrating Relighting and dynamic mesh subdivision to handle complex topological changes.
Conclusion
GaussCraft proves that rigged 2D Gaussians are a powerful representation for editable 3D scenes. By anchoring Gaussians to an explicit mesh and optimizing with geometric regularizers, we provide a foundation for the next generation of real-time, interactive digital content creation.
