[Paper Review] GaussianAvatars: Photorealistic Head Avatars with Rigged 3D Gaussians

Introduction
In this post, I review GaussianAvatars: Photorealistic Head Avatars with Rigged 3D Gaussians, a recent paper presented at CVPR 2024 by Shenhan Qian et al. This work builds on the success of 3D Gaussian Splatting and extends it to model photorealistic dynamic head avatars using a rigged and animatable 3D Gaussian-based representation. Unlike static scene models, GaussianAvatars focuses on realistic facial expressions, head motion, and view-dependent appearance, making it a powerful tool for virtual telepresence, AR/VR, and character animation.
Paper Info
- Title: GaussianAvatars: Photorealistic Head Avatars with Rigged 3D Gaussians
- Authors: Shenhan Qian, Tobias Kirschstein, Liam Schoneveld, Davide Davoli, Simon Giebenhain, Matthias Nießner
- Conference: CVPR 2024
- Paper Link: ArXiv:2312.02069
Motivation
Previous works like Neural Radiance Fields (NeRF) and 3D Gaussian Splatting (3DGS) excel at rendering static scenes, but they struggle with:
- Real-time performance
- Animatable human models
- High-fidelity rendering under dynamic conditions (e.g., expressions, head turns)
GaussianAvatars address these limitations by introducing:
- A dynamic, rigged 3D Gaussian representation
- Blendshape-based expression modeling
- An efficient rasterization pipeline for real-time rendering
Method Overview
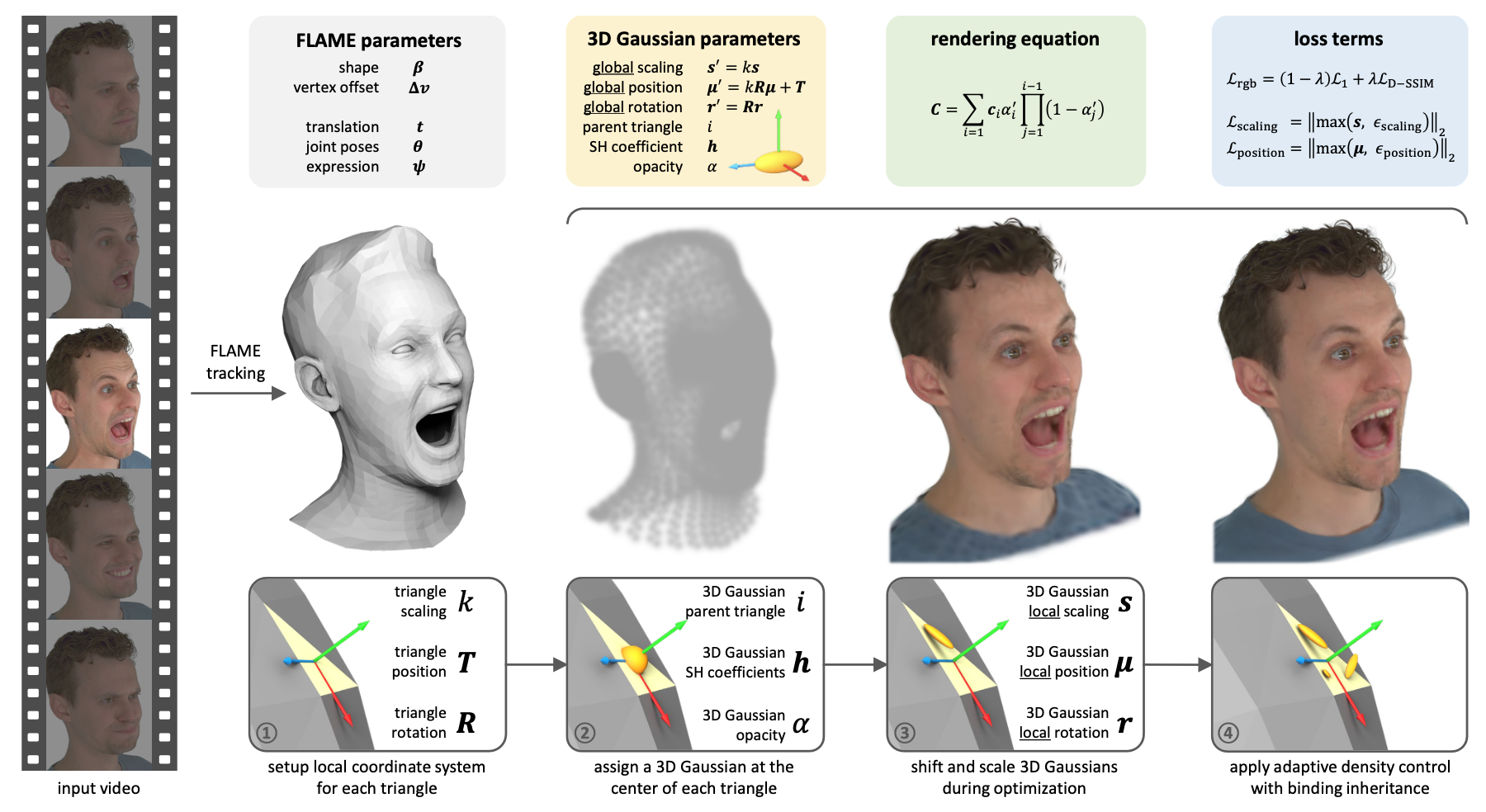
1. Rigged 3D Gaussian Representation
GaussianAvatars extend 3D Gaussian Splatting by rigging each Gaussian to a triangle in the FLAME mesh. Unlike NeRFs or earlier splatting methods where Gaussians are fixed in world space, here each Gaussian lives in the local coordinate system of a triangle and moves as the triangle deforms over time (due to pose or expression changes).
🧱 Local Frame Construction
Each triangle defines a local coordinate system:
- Let the triangle vertices be \(\{v_1, v_2, v_3\}\)
- The local origin T is the mean of the vertices.
- Construct a rotation matrix \(R \in \mathbb{R}^{3 \times 3}\) from:
- Edge direction \(e = v_2 - v_1\)
- Normal \(n = (v_2 - v_1) \times (v_3 - v_1)\)
- Cross product of the two: \(e \times n\)
- The triangle scale \(k\) is computed from the average edge length and its perpendicular, capturing the local size.
🧩 Gaussian Parameters in Local Space
Each Gaussian is defined in triangle-local space with:
- Local position \(\mu\)
- Local rotation r
- Local scale s
At render time, these are converted to global space:
\[r' = R \cdot r \\ \mu' = k \cdot R \cdot \mu + T \\ s' = k \cdot s\]This formulation ensures that Gaussians deform smoothly and naturally as the triangle moves due to FLAME-driven articulation.
It also has optimization benefits: since the parameters are relative to local triangle scale, Gaussians on small triangles move less per step than those on large ones, enabling consistent learning rates across varying mesh regions.
2. View-Dependent Appearance Modeling
Each Gaussian defines an appearance function:
\[F(x, v) \rightarrow (r, g, b, \alpha)\]Where:
- x : 3D Gaussian center in world space
- v : camera/viewing direction
- (r, g, b) : RGB appearance
- \(\alpha\): opacity
This function is parameterized using low-dimensional view-dependent appearance bases, e.g., spherical harmonics (SH) or learned MLP embeddings. It enables:
- View-consistent shading
- Specular highlights
- Smooth blending during splatting
🧬 Binding Inheritance (Adaptive Density Control)
The initial rig attaches one Gaussian per triangle, but this is insufficient to represent fine details like hair strands or creases. GaussianAvatars adopt adaptive density control from [3DGS], enhanced by a novel binding inheritance strategy:
- Gaussians are split or cloned based on:
- High view-space positional gradient
- Opacity threshold
- New Gaussians are added in the local space of their parent triangle.
- Each Gaussian stores the index of its parent triangle to support:
- Inherited rig binding when new Gaussians are added
- Consistency in motion during animation
To prevent degeneration:
- A pruning step resets or deletes low-opacity Gaussians
- To protect occluded regions (like teeth or eyeballs), a constraint ensures each triangle always has at least one Gaussian attached
This results in a dynamic, detail-preserving, and animation-consistent Gaussian representation.
3. Training Pipeline
GaussianAvatars build on 3D Gaussian Splatting (3DGS) by integrating a FLAME-based rig, allowing expressions and poses to animate Gaussians through mesh-driven deformation. However, this introduces new optimization challenges, such as misalignment artifacts and scaling instability, especially under animation. To solve this, the authors propose a custom loss function with new geometric regularizers and a perceptual similarity term.
📦 Overall Loss Function
The full loss used during training is:
\[\mathcal{L} = \mathcal{L}_{\text{rgb}} + \lambda_{\text{position}} \mathcal{L}_{\text{position}} + \lambda_{\text{scaling}} \mathcal{L}_{\text{scaling}}\]Where:
- \(\mathcal{L}_{\text{rgb}}\) is the image reconstruction loss
- \(\mathcal{L}_{\text{position}}\) constrains Gaussians to stay near their mesh triangle
- \(\mathcal{L}_{\text{scaling}}\) prevents overly large Gaussians from causing animation instability
🎨 RGB Reconstruction Loss
The RGB loss blends pixel-wise L1 and a structural dissimilarity (D-SSIM) term:
\[\mathcal{L}_{\text{rgb}} = (1 - \lambda) \cdot \mathcal{L}_{1} + \lambda \cdot \mathcal{L}_{\text{D-SSIM}}\]Where \(\lambda = 0.2\). This combination captures both pixel-level accuracy and perceptual structure, providing better rendering quality without additional silhouette or depth supervision.
📍 Position Loss
To ensure Gaussians remain near their parent triangle in the FLAME mesh, the position loss applies a soft constraint:
\[\mathcal{L}_{\text{position}} = \| \max(\mu, \epsilon_{\text{position}}) \|_2\]Where:
- \(\mu\) is the offset vector between a Gaussian and its corresponding triangle center
- \(\epsilon_{\text{position}} = 1\) defines a threshold under which errors are ignored
This avoids wild spatial drift when Gaussians are animated.
📏 Scaling Loss
Large Gaussians can introduce visual jitter when their associated triangles rotate slightly. To address this, a scale-based penalty is added:
\[\mathcal{L}_{\text{scaling}} = \| \max(s, \epsilon_{\text{scaling}}) \|_2\]Where:
- \(s\) is the Gaussian’s scale relative to the triangle scale
- \(\epsilon_{\text{scaling}} = 0.6\) disables the penalty when Gaussians are reasonably small
This prevents excessive jitter and improves runtime performance by limiting the number of splats intersected by a ray.
🛠 Optimization Details
- Optimizer: Adam
- Learning rate:
- 5e-3 for position
- 1.7e-2 for scale
- Fine-tuned FLAME params (translation, pose, expression) at 1e-6 to 1e-3
- Gaussians’ opacity is reset every 60k iterations to improve convergence
- Training runs for 600k iterations with exponential learning rate decay
- Adaptive density control with binding inheritance is enabled from 10k to 600k iterations (every 2k steps)
These new regularization terms and adaptive training behaviors are crucial to maintaining structural consistency and animation stability while still benefiting from the efficient rasterization pipeline of 3DGS.
4. Real-Time Rendering via Splatting
GaussianAvatars preserve the rasterization and splatting pipeline from 3DGS, but extend it to support expression-dependent Gaussian deformation.
🧠 Deformation-aware Splatting
The projection of each deformed Gaussian becomes:
\[\mathbf{u}_j = \mathbf{P} \cdot \mathbf{x}_j(\mathbf{w})\]and its 2D projected covariance is:
\[\Sigma_j^{(2D)}(\mathbf{w}) = J_j(\mathbf{w}) \Sigma_j J_j(\mathbf{w})^\top\]Rendering is done using the over-operator:
\[\hat{I}(\mathbf{u}) = \sum_{j} T_j(\mathbf{u}) \cdot \alpha_j \cdot F_j(x_j(\mathbf{w}), v)\]Where transmittance is defined as:
\[T_j(\mathbf{u}) = \prod_{k < j} (1 - \alpha_k)\]Key Contributions
-
Triangle-Rigged 3D Gaussian Avatar Representation: The first method to rig 3D Gaussians to a parametric mesh (FLAME) using triangle-local coordinate systems, enabling stable and expressive head avatar animation.
-
Binding Inheritance for Adaptive Density Control: A novel mechanism that ensures newly added Gaussians (via densification) inherit the rigging of their parent triangle, preserving local controllability and structural coherence across animation.
Results
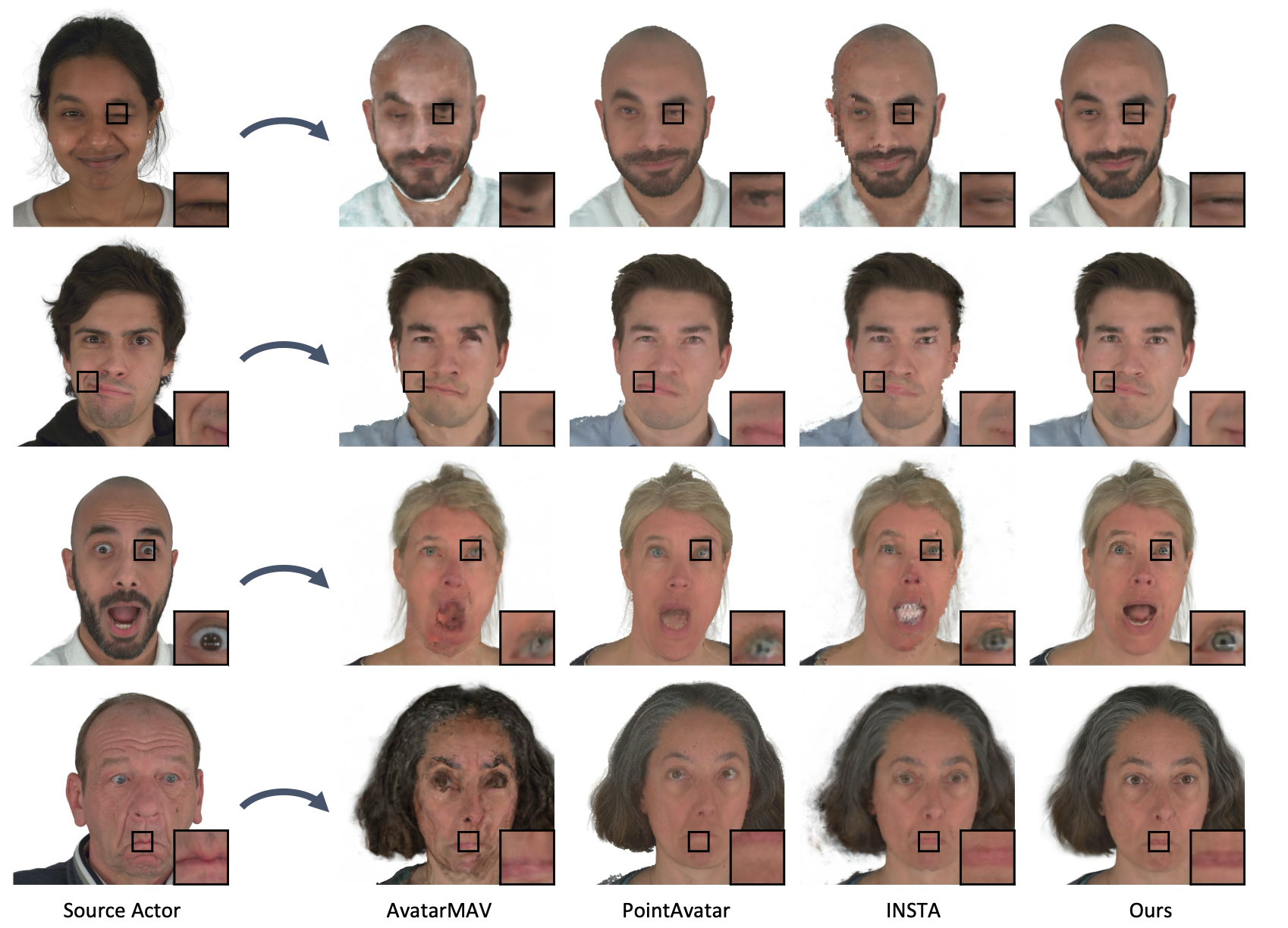
- Outperforms NeRF and other neural rendering methods in speed, visual quality, and animatability
- Produces photorealistic facial renderings with subtle expression dynamics
- Can generalize across expressions not seen during training
Limitations and Future Work
- Limited to head-only avatars; extending to full body or upper body remains an open challenge
- Requires multi-view data for training
- Generalization to novel subjects is not addressed (subject-specific training)
Future directions may include:
- Full-body avatars using similar Gaussian rigs
- Expression transfer between identities
- Few-shot personalization with monocular input
Conclusion
GaussianAvatars demonstrate that rigged 3D Gaussians can be used not just for static scenes, but also for high-quality dynamic facial avatars. This work significantly pushes forward the frontier in real-time neural rendering and avatar modeling, offering a promising foundation for virtual humans, telepresence, and digital actors.
