[Paper Review] NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis

Introduction

In this post, I review the influential paper “NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis” by Mildenhall et al., which introduced a novel way to synthesize novel views of complex 3D scenes using neural networks.

Paper Info

• Title: NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis
• Authors: Ben Mildenhall, Pratul P. Srinivasan, Matthew Tancik, Jonathan T. Barron, Ravi Ramamoorthi, Ren Ng
• Conference: ECCV 2020
• Paper: NeRF

Motivation

Traditional view synthesis methods rely on multi-view stereo or explicit geometry. However, these approaches often fail in scenes with complex geometry or view-dependent effects like reflections. NeRF addresses this by learning a volumetric scene representation entirely through a neural network trained to render photorealistic novel views.

Core Idea

NeRF models a scene as a continuous 5D function:

\[F(x, d) \rightarrow (r, g, b, \sigma)\]

Where:

• x ∈ ℝ³ is the 3D coordinate
• d ∈ ℝ² is the viewing direction (encoded as a 2D direction vector)
• (r, g, b) is the emitted RGB color
• σ is the volume density at point x

This function is represented by a fully-connected neural network trained with a volumetric rendering loss using multiple posed images.

Network Architecture and Encoding

To enable the MLP to learn complex geometry and high-frequency details, NeRF applies two essential techniques: positional encoding and view-dependent color prediction.

Positional Encoding

One challenge NeRF faces is that MLPs struggle to learn high-frequency functions directly from raw 3D coordinates. To address this, NeRF applies positional encoding to the input coordinates before feeding them into the network.

Instead of using the raw coordinate \(x \in \mathbb{R}^3\), NeRF encodes each dimension with a set of sinusoidal functions:

\[\gamma(p) = [\sin(2^0 \pi p), \cos(2^0 \pi p), \ldots, \sin(2^{L-1} \pi p), \cos(2^{L-1} \pi p)]\]

This Fourier feature mapping helps the MLP represent high-frequency details (e.g., sharp edges, fine texture) by making it easier to learn complex variations in the scene.

• Typical setting: \(L = 10\) for position, \(L = 4\) for viewing direction

View Dependence (Modeling Non-Lambertian Surfaces)

Real-world objects often exhibit view-dependent effects, such as specular highlights or reflections. NeRF handles this by making the emitted color a function of both position and viewing direction:

• The density \(\sigma\) is predicted only from the 3D point \(x\)
• The RGB color \((r, g, b)\) is predicted from both \(x\) and the encoded viewing direction \(d\)

To achieve this:

• The network splits into two branches:
  1. One MLP branch encodes spatial geometry and density
  2. Another branch takes the learned features from the geometry MLP + view direction to output color

This enables NeRF to render complex materials—such as shiny, glossy, or translucent surfaces—more realistically than models that ignore view dependence. The impact of positional encoding and view-dependent rendering is illustrated in the figure below, which shows a bulldozer scene from the original paper.

Training

NeRF optimizes the parameters of the MLP by minimizing the difference between rendered and ground-truth pixel colors. It uses hierarchical volume sampling:

• A coarse network samples points uniformly along each ray
• A fine network samples more points where density is higher

Results

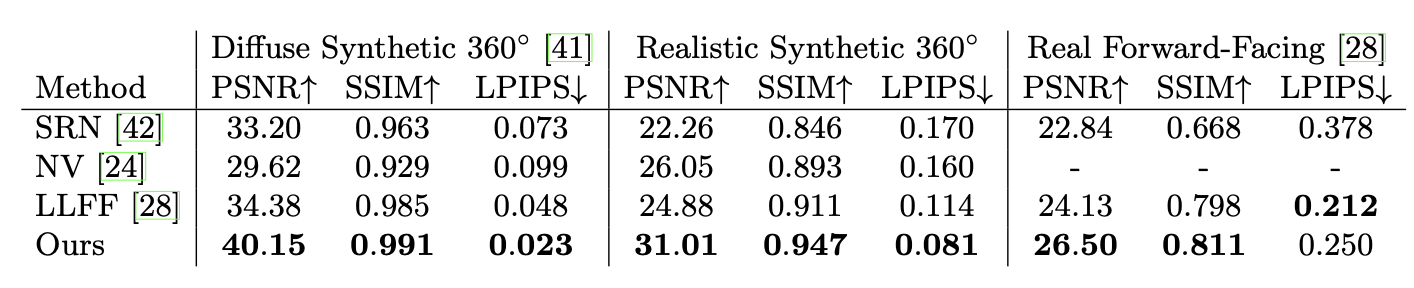
NeRF achieves state-of-the-art view synthesis quality on forward-facing and 360° datasets. It can synthesize realistic novel views with correct parallax, lighting, and fine detail.

Limitations

• Long training time (several hours per scene)
• Requires precise camera poses
• Cannot handle dynamic scenes
• Computationally expensive rendering

Impact

NeRF inspired a huge number of follow-up works, including:

• Mip-NeRF (faster and better generalization)
• Instant-NGP (real-time training)

Conclusion

NeRF is a landmark paper in 3D vision and neural rendering. It redefined how we think about scene representation and opened up an entirely new line of research into implicit 3D modeling.

---

Next: I’ll be reviewing its fast variants and generalization methods like Mip-NeRF and PixelNeRF.